题目解析

找到数组中重复的元素，难点在于不能修改原数组、空间复杂度O(1)、时间复杂度小于O(n^2)

方法

在这里一共n个元素，有n+1种元素，因为重复元素可以多于1，说明每个元素最多能有n-1个能放在对应索引上。
如果将元素的值作为索引，可以发现规律，比如：

1
2
3
4
5
输入: [1,3,4,2,2]
可以看成：
索引：0 1 2 3 4
  值：1 3 4 2 2

将index和nums[index]看成index->nums[index]，将这个数组变成链表，上面的输入可以看成0->1->3->2->4->2，可以发现有一个环，这是因为多了一个重复的数i，在某个索引j上nums[j]为i。这样就可以使用这道链表题目的思路题目

首先有两个结论，对于快慢两个指针fast、slow，fast一次走两步，slow一次走一步：

  1. fast和slow会在环里面碰面，碰面地点是pos。此时slow走的距离是s，fast走过的距离是2s，因为fast一次走两步。
  2. slow到环口的距离与环口到链表开始节点的距离相同，也就是此时再有一个指针m，与slow同时往前走，会在环口相遇。
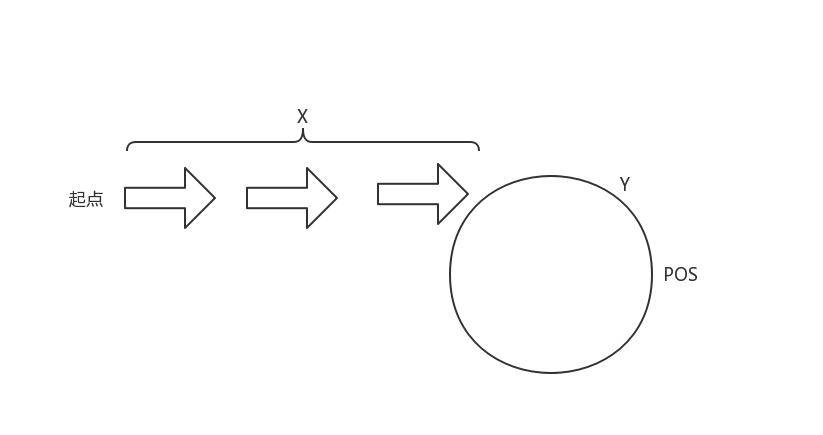
    令： x为开始节点到环口的距离，y为环口到第一次相遇节点pos的距离，C为环的周长
    证明：
  • slow走的距离s = x + y
  • fast走的距离2s = x + y + n*C (nC表示在环里走了很多次)
  • 两式相减得 x = n*C - y = C - y，C-y是slow继续走到环口需要的距离
  • 可得:slow到环口的距离与环口到链表开始节点的距离相同
    链表模拟
    时间复杂度O(N)，空间复杂度O(1)
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    class Solution {
    public:
        int findDuplicate(vector<int>& nums) {
            if (nums.size() < 2) return -1;
            int fast = 0;
            int slow = 0;
            do{
                fast = nums[nums[fast]];
                slow = nums[slow];
            }while (fast != slow) ;
            int i = 0;
            while (i != slow) {
                i = nums[i];
                slow = nums[slow];
            }
            return i;
        }
    };